Kapitel 4
Gravitation
Was wissen wir über die Gravitation?
Alle Körper ziehen sich aufgrund ihrer Massen gegenseitig an. So zieht z.B. die Erde den Mond an. Umgekehrt zieht auch der Mond die Erde an.
Die gegenseitige Anziehung von Körpern aufgrund ihrer Massen wird Massenanziehung oder Gravitation (gravis, lat.: schwer) genannt.
Die dabei wirkenden Kräfte werden als Schwerkräfte oder als Gravitationskräfte bezeichnet. https://www.lernhelfer.de/schuelerlexikon/physik-abitur/artikel/gravitation-und-gravitationsgesetz
Die Gravitationskraft zwischen zwei Körpern kann man mithilfe des Gravitationsgesetzes gerechnet werden. Dieses Gesetz wurde von dem englischen Naturforscher Isaac Newton (1643- 1727) um das Jahr 1687 festgestellt (Abb.28).
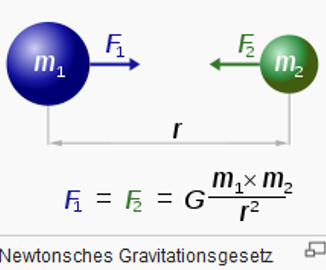
Abbildung 34: Newtonsches Gravitationsgesetz
Dieses Gesetz wurde durch die zahlreichen Experimenten und Beobachtungen entdeckt und beschrieben.
Gemäß den letzten Beobachtungen von den Sternen und Galaxien entstand eine neue Mond- Theorie, die quadratische Abnahme der Anziehungskräfte infrage stellt.
„In der Modifizierten Newtonschen Dynamik (MOND) wechselt die Schwerkraft unterhalb eines bestimmten Grenzwerts von der quadratischen Abnahme zu einer Abnahme, die flache Rotationskurven reproduziert“.
https://www.spektrum.de/alias/bilder/was-steckt-hinter-der-dunklen-materie/1437830
Die Gravitationskonstante (G) wird immer wieder mit den modernen Technologien neu berechnet. Mithilfe laser-gekühlter Atome in einem Quanteninterferometer erhielten die Wissenschaftler jetzt einen Wert von 6,67191∙10^-11 m^3/kgs^2, der damit etwas kleiner ist als der derzeitige Standardwert 6,67384∙10^-11 m^3/kgs^2
Es wurde nie bewiesen, ob sich zwei Körper gegenseitig anziehen, oder aufeinander zudrücken werden. Es ist nur eine wissenschaftliche Behauptung und Annahme (Postulat).
Wie eine Gravitation entsteht und welche Kräfte in diesem Fall verwendet werden, werden wir jetzt erläutern.
Um nicht essenzielle Momente auszuschließen und den Mechanismus der Gravitation in unseren weiteren Erklärungen besser zu verstehen, machen wir eine Annahme:
Nehmen wir an, dass die Geschwindigkeiten (kinetische Energie) aller Neutrinos im Universum und die Dichte ihrer Ausbreitungen in allen Richtungen gleich sind.
Das bedeutet, dass wir die resultierende Kraft (𝑭𝑹𝒆𝒔.), die für die kosmische Expansion des Universums verantwortlich ist, aus unserer Betrachtung ausschließen und betrachten sie als gleich null.
Ich möchte nun daran erinnern, dass das Neutrino, das ein Atom durchdringt, verliert
ein winziger Teil seiner kinetischen Energie. Gleichzeitig wird diese Energie dafür verwendet, das Atom in die Richtung des Neutrino Fluges zu bewegen.
Abbildung 35 zeigt zwei Himmelskörper, die sich in einem bestimmten Abstand voneinander befinden. Diese Körper könnten zum Beispiel die Erde und der Mond sein.
Auf jedes Neutrino, das einen einzelnen Himmelskörper von einer bestimmten Seite trifft, gibt es immer ein entgegengesetzt propagierendes Neutrino, das es vollständig neutralisiert (dank unserer Annahme, dass die kinetischen Energien und Neutrino Dichten auf allen Seiten gleich sind). Infolgedessen ist ein alleinstehender Himmelskörper im Weltraum keinem mechanischen Effekt des Neutrinos ausgesetzt (𝑭𝑹𝒆𝒔. = 0) und bleibt in Ruhe.
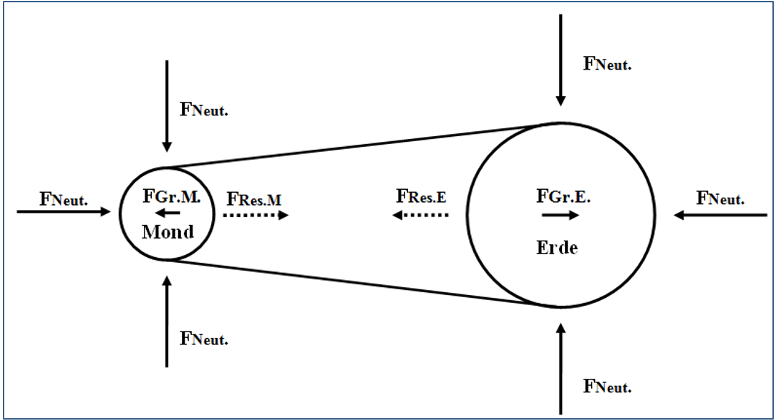
Abbildung 35: Neutrinos, die die Erde und den Mond von allen Seiten durchbohren, erzeugen die resultierenden Kräfte, die aufeinander gerichtet sind
In unserem Fall, der in Abbildung 35 dargestellt ist, sehen wir keinen einzigen Himmelskörper, sondern zwei benachbarte Objekte (Erde und Mond). Diese beiden Objekte erzeugen eine gewisse Barriere für den Neutrino Fluss von einer Seite, wodurch ein sogenannter Schatten entsteht.
⃗
Die Stärke des Neutrinoeffekts (𝑭𝑵𝒆𝒖𝒕.) ist eine Vektorgröße. Da wir nur die Einflüsse der entgegenfliegenden Neutrinos betrachten, werden wir im Folgenden nicht das Vorzeichen des Vektors angeben.
Machen wir noch eine kleine Annahme:
Hier werden wir keine Neutrinos berücksichtigen, die auf die beschattete Seite des Himmelskörpers treffen, ohne zuvor durch einen anderen Himmelskörper durchquert zu haben. Solche Neutrinos treffen die beschattete Seite des Körpers direkt aus dem Weltraum mit voller Kraft 𝑭𝑵𝒆𝒖𝒕. (Abb.36 ein roter Bereich) und werden, wie wir oben erwähnt haben, von entgegenfliegenden Neutrinos voll neutralisiert.
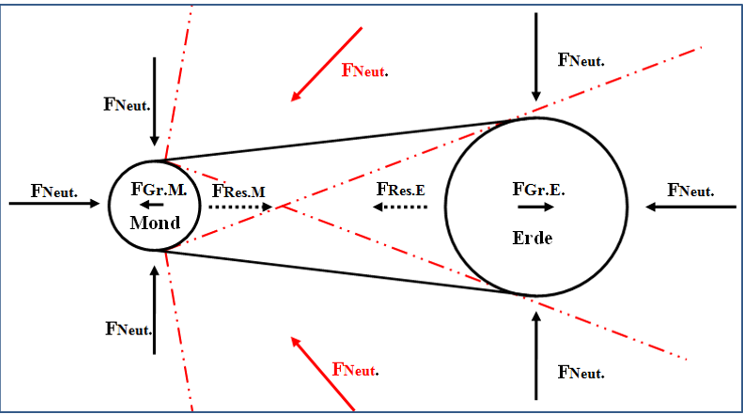
Abbildung 36: Neutrinos, die Himmelskörper direkt aus dem Weltraum durchdringen und aufeinander gerichtet sind, werden vollständig neutralisiert
Je größer ist der Abstand zwischen den beiden Körpern, desto höherer Prozentsatz der vollen Neutrinos (𝑭𝑵𝒆𝒖𝒕.) ist, die auf die beschattete Seite des Körpers treffen, ohne zuerst durch einen anderen Körper geflogen zu haben.
Und dies wiederum reduziert prozentual die Anzahl der Neutrinos, die durch den ersten Himmelskörper fliegen und dadurch geschwächt auf den zweiten Körper fallen. Infolgedessen werden die resultierenden Kräfte, die auf jeden Himmelskörper individuell wirken, ebenfalls abnehmen.
Um das Verständnis des Gravitationsprinzips zu vereinfachen, betrachten wir nur 6 Neutrinos (Abb.35).
Wie wir wissen, gehen die Neutrinos leicht durch die großen Schichtdicken hindurch.
Ein bestimmter Kleinteil der Energiekraft des Neutrinos (z. B. 𝑭𝑮𝒓.𝑬), der von der Dichte und der Größe des Himmelskörpers (z. B. Erde) abhängig ist, geht verloren, um den Widerstand aller auf dem Weg des Teilchens liegenden Atome zu überwinden.
Mit gebliebener Kraft (𝑭𝑹𝒆𝒔.𝑬 = 𝑭𝑵𝒆𝒖𝒕. − 𝑭𝑮𝒓.𝑬) fliegt das Neutrino weiter und trifft den anderen Himmelskörper (z. B. Mond).
Andererseits, das Neutrino, das durch den Mond passiert ist, greift auch die Erde mit der geschwächten Kraft ( 𝑭𝑹𝒆𝒔.𝑴 = 𝑭𝑵𝒆𝒖𝒕. − 𝑭𝑮𝒓.𝑴) an.
Diesen kleinen Teil der Energiekraft des Neutrinos, der im Körper geblieben ist, nennen wir Schwerkraft oder Gravitationskraft 𝑭𝑮𝒓. des Körpers.
Den Rest der Energiekraft, die von anderer Seite des Himmelskörpers rausgeht, nennen wir Restkraft des Neutrinos (𝑭𝑹𝒆𝒔.).
Für die Erde: 𝑭𝑹𝒆𝒔.𝑬 = 𝑭𝑵𝒆𝒖𝒕. − 𝑭𝑮𝒓.𝑬
Für den Mond: 𝑭𝑹𝒆𝒔.𝑴 = 𝑭𝑵𝒆𝒖𝒕. − 𝑭𝑮𝒓.𝑴
Nun betrachten wir separat die Kräfte, die auf die Erde von allen Seiten eintreffen. Dann summieren wir alle vektoriellen Kräfte und rechnen eine resultierende vektorielle Kraft (𝑭𝑬𝒓𝒅𝒆) aus, die die Erde in Bewegung treibt.
Die Kräfte (𝑭𝑵𝒆𝒖𝒕.), die von oben und von unten mit vollen und gleichen Größen die Erde durchrasen, werden gegenseitig aufgehoben.
Die Seite der Erde, die im Schatten des Mondes liegt, empfängt Neutrinos (𝑭𝑹𝒆𝒔.𝑴), die zuvor durch die Dicke des Mondes geflogen sind.
Die resultierende vektorielle Kraft (𝑭𝑬𝒓𝒅𝒆), die auf die Erde ausgeübt wird, rechnet sich aus:
𝑭𝑬𝒓𝒅𝒆 = 𝑭𝑵𝒆𝒖𝒕. − 𝑭𝑹𝒆𝒔.𝑴 = 𝑭𝑵𝒆𝒖𝒕. − (𝑭𝑵𝒆𝒖𝒕. − 𝑭𝑮𝒓.𝑴) = 𝑭𝑮𝒓.𝑴
𝑭𝑬𝒓𝒅𝒆 = 𝑭𝑮𝒓.𝑴
Somit wird die Erde, die im Schatten des Mondes liegt, mit der Kraft 𝑭𝑬𝒓𝒅𝒆 zum Mond tendieren, die die gleiche Größe wie die Gravitationskraft des Mondes 𝑭𝑮𝒓.𝑴 hat.
Und die resultierende vektorielle Kraft, die auf den Mond ausgeübt wird (𝑭𝑴𝒐𝒏𝒅), rechnet sich aus:
𝑭𝑴𝒐𝒏𝒅 = 𝑭𝑵𝒆𝒖𝒕. − 𝑭𝑹𝒆𝒔.𝑬 = 𝑭𝑵𝒆𝒖𝒕. − (𝑭𝑵𝒆𝒖𝒕. − 𝑭𝑮𝒓.𝑬) = 𝑭𝑮𝒓.𝑬
𝑭𝑴𝒐𝒏𝒅 = 𝑭𝑮𝒓.𝑬
Dies bedeutet, dass der Mond mit der gleichen Kraft wie die Gravitationskraft der Erde zur Erde gedrückt wird.
Um diesen ungewöhnlichen Ausdruck wie Kraft des Schiebens zu vermeiden, nehmen wir an, dass die Erde den Mond mit der eigenen Gravitationskraft zu sich zieht. Das Ergebnis ändert sich nicht, aber den gewöhnlichen Ausdruck wie „Anziehungskraft“ könnte man weiter benutzen. Es muss nur klar verstanden werden, was sich hinter diesem Begriff verbirgt.
Die gesamte Anziehungskraft zwischen die Erde und den Mond (Gravitationskraft) rechnet sich so aus:
𝑭𝑮𝒓. = 𝑭𝑮𝒓.𝑬 + 𝑭𝑮𝒓.𝑴
Diesen Gravitationseffekt kann man auch als Schatteneffekt bezeichnen. Jeder Himmelskörper (z. B. die Erde und der Mond) liegt im Schatten des anderen Körpers. Nur dank dieses Schatteneffekts, ergibt sich die Anziehungskraft, die auch als Gravitation benennen werden kann.
Im Sonnensystem bestimmt die Gravitation (die Schatteneffekt) die Bahnen der Planeten, Monde, Kometen, Satelliten und im Kosmos die Bildung von Sternen und Galaxien.
Und jetzt folgt ein wichtiger Punkt!
Wie wir bereits erwähnt haben, gilt die Formel der Gravitation mit voller Wirkung der Kräfte auf andere Körper nur dann, wenn die beiden Himmelskörper ganz nah zueinander stehen (L = 0) (Abb.37).
Die Zunahme des Abstandes zwischen den beiden Himmelskörpern (L > 0) führt zu einer prozentualen Zunahme der Neutrinos, die direkt aus dem Weltraum kommen und mit voller Kraft (𝑭𝑵𝒆𝒖𝒕.) den Körper durchfliegen. Die Auswirkungen solcher Neutrinos werden durch entgegenfliegenden Neutrinos vollständig zunichtegemacht.
Daraus folgt, dass die „Anziehungskraft“ sinkt.
Solange es in unserem Sonnensystem passiert, ist das Newtonschen Gravitationsgesetz (Abb.34) immer noch aktuell.
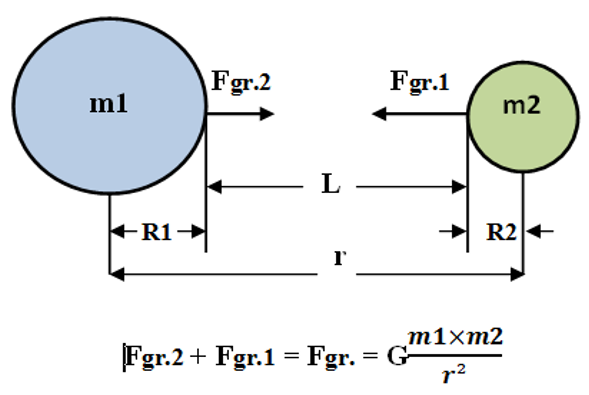
Abbildung 37: Das Gesetz der Schwerkraft
Hier Fgr.1 ≠ Fgr.2, weil m1 ≠ m2 r = R1+R2+L
G: Gravitationskonstante gleich 6,67430(15) · 10^−11 м3/s^2·кг.
Die Höhen der Gravitationskräften Fgr.1 und Fgr.2 hängen nicht nur von den Massen der Körper, sondern auch von der Neutrinos Dichte (Teilchenkonzentration) ab, die im unseren nah liegenden Bereich des Sonnensystems sich nicht wirklich ändert.
Deswegen Gravitationskonstante, die wiederum aus diesen Kräften ausgerechnet wurde, bleibt auch konstant.
Die Gravitationskonstanten irgendwo an der anderen Seite der Galaxie oder des Weltraumes werden bestimmt ganz andere Werte haben!
Mit gleicher Vorgehensweise kann man die Gravitation der Erde sowie die Gewichtskraft eines Körpers, der sich auf der Erde befindet, erklären (Abb.38).
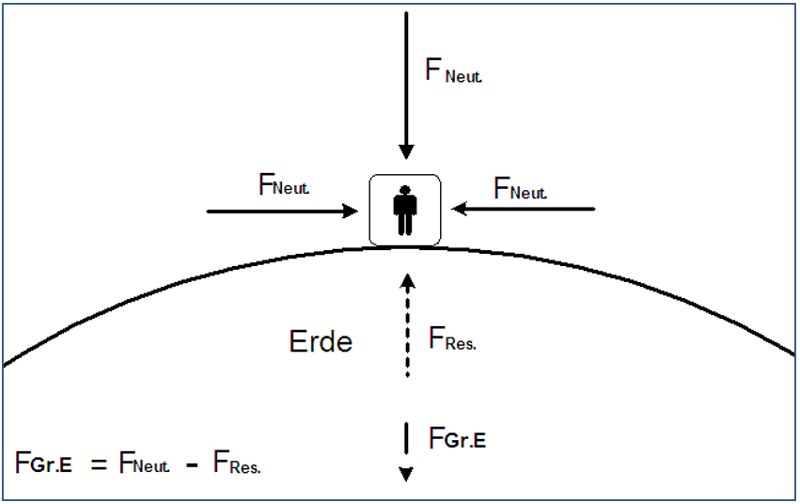
Abbildung 38: Körpergewicht auf der Erdoberfläche
Die Gewichtskraft gibt an, wie stark ein Körper konkret von der Erde oder vom anderen Himmelskörper, auf dem er sich befindet, angezogen wird.
Die Gewichtskraft (𝑭𝑮) eines Körpers (z. B. einen Menschen) auf der Erde setzt sich aus drei Kräften zusammen:
- Eine Gravitationskraft der Erde 𝑭𝑮𝒓.𝑬, mit der sich dieser Körper durch die Neutrinos, die von oben in die Richtung des Mittelpunktes der Erde kommen, zugedrückt wird.
- Eine Gravitationskraft des Körpers 𝑭𝑮𝒓.𝑲, mit der sich die Erde durch die Neutrinos, die von anderer Seite der Erde in die Richtung des Körpers fliegen, zugedrückt wird.
- Die Zentrifugalkraft 𝑭𝒁𝒆𝒏𝒕𝒓., die wegen der Rotation der Erde entstanden ist. Diese Kraft verkleinert die Gewichtskraft des Körpers.
𝑭𝑮 = 𝑭𝑮𝒓.𝑬 + 𝑭𝑮𝒓.𝑲 − 𝑭𝒁𝒆𝒏𝒕𝒓.
Die Zentrifugalkraft FZentr ist im Vergleich zur Gravitationskraft der Erde 𝑭𝑮𝒓.𝑬 in unserem Fall ziemlich klein und wir werden sie weiter nicht berücksichtigen.
𝑭𝑮 = 𝑭𝑮𝒓.𝑬 + 𝑭𝑮𝒓.𝑲 = 𝑮 ∙ 𝒎𝑲 ∙ 𝒎𝑬 / 𝒓^𝟐
𝑮 ∙ 𝒎𝑬 /𝒓^𝟐 = 𝐠
𝐠: Die Gravitationsbeschleunigung [m/s^2].
Dann die Gewichtskraft des Körpers (wie wir schon immer gewusst haben) kann als Produkt seiner Masse (𝒎) und der Schwerebeschleunigung (𝐠) der Erde berechnet werden:
𝑭𝑮 = 𝒎𝐠
Die Schwerebeschleunigung (die Fallbeschleunigung) an einem bestimmten Punkt des Weltraumes kann man mit der Hilfe des Gravimeters bestimmen.
Die Gravitationsbeschleunigung (𝐠) hängt von der Gravitationskonstante (𝑮), der Masse des Himmelskörpers (𝒎) und dem Quadrat der Entfernung (𝒓^𝟐) davon ab.
Auf der Erdoberfläche beträgt die Fallbeschleunigung: 𝐠 = 9,81 m/s^2
Auf dem Mond: 𝐠 = 1,62 m/s^2
Im Vakuum des Kosmos (In der Schwerelosigkeit): 𝐠 = 0 m/s^2
Die Masse (𝒎 = 𝛒𝐕) hängt von der Dichte und dem Volumen des Körpers und nicht von seinem Aufenthaltsort (Erde, Mond, Schwerelosigkeit...) ab.
Die Dichte hängt von den atomaren Strukturen des chemischen Elements des Körpers ab.
Nur die Gewichtskraft 𝑭𝑮 hängt vom Aufenthaltsort des Stoffes (𝑭𝑮 = 𝒎𝐠) ab.
Bei der Masse m = 10 kg ist die Gewichtskraft:
- Auf der Erde 𝑭𝑮 = 10 kg ⋅ 9,81 m/s^2 = 98,1 N.
- Auf dem Mond 𝑭𝑮 = 10 kg ⋅ 1,62 m/s^2 = 16,21 N.
- In der Schwerelosigkeit 𝑭𝑮 = 10 kg ⋅ 0 m/s^2 = 0 N.
Kapitel 5
Wieso ist es so schwer Neutrinos aufzuspüren?
Obwohl mehr als 65 Milliarden Neutrinos durch jeden Quadratzentimeter der Erdfläche pro Sekunde hindurch rasen, kollidieren sie mit den Kernteilchen (Quarks) sehr selten. Wieso?
Da der Radius der Atomhülle im Vergleich zum Radius der Atomkerne (Quarks) in 100 000-mal größer ist, ist die Wahrscheinlichkeit, dass das Neutrino direkt die Atomkerne treffen würde, ziemlich gering. Aber die Zahl der Atome, die dieses Neutrino in seinem Flug durch die ganze Erde sie durchquert, ist viel-viel größer. Deswegen sollte die Kollisionswahrscheinlichkeit eigentlich nah zu 100 % sein.
Es gibt bestimmt eine andere Ursache, die Zusammenstoßen der Teilchen vermeiden lässt. Und diese Ursache werden wir jetzt ermitteln.
Es ist schon bekannt, dass die Zahl der Neutrinos, die unsere Erde ohne Kollision durchdringen, von der Energie der Neutrinos abhängt.
Mit zunehmender Energie nimmt die Kollisionswahrscheinlichkeit der Neutrinos zu und die mittlere freie Weglänge entsprechend ab.
„Bei 1000 TeV Energie beträgt die mittlere freie Weglänge der Neutrinos in der Erde etwa einen Erddurchmesser. Das bedeutet, dass bei einem Flug senkrecht durch die Erde etwa zwei Drittel solcher Neutrinos wechselwirken, während ein Drittel ungehindert durch die Erde durchfliegt. Bei 11 MeV ist die mittlere freie Weglänge in Blei bereits 350 Milliarden km, und in der Erde würden von einer Milliarde Neutrinos im Schnitt etwa drei eine Wechselwirkung eingehen, während die restlichen ungehindert durchfliegen.“
Da das Neutrino ein Teilchen ist, das eine Masse m = 4,19 · 10−31 kg besitzt und mit der hohen Geschwindigkeit durch das Vakuum (Gluonen-Substanz) fliegt, sollte zwischen denen eine bestimmte Wechselwirkung entstehen.
Da das Neutrino das gleiche Teilchen wie der Quark ist, erfolgt der Prozess der Umverteilung von Impulsen mit Gluonen auf ähnliche Weise. Gluon wird mit der gleichen Lichtgeschwindigkeit reflektiert, und das Neutrino erhält einen Impulsvektor 𝝆𝒈𝒍. = 𝒎𝒈𝒍.𝒄𝒈𝒍. = 𝟏, 𝟐𝟔 · 𝟏𝟎−𝟒𝟔 𝐤𝐠𝒎/s, der mit einer linearen Geschwindigkeit von 𝟑 ⋅ 𝟏𝟎−𝟏𝟔 m s^-1, auf das Zentrum des Teilchens gerichtet ist.
Dieser winzige Geschwindigkeitsvektor, der dem Neutrino-Geschwindigkeitsvektor hinzugefügt wird, ändert sofort seine Flugrichtung. Natürlich ist diese Einstellung sehr unbedeutend, aber wenn es ziemlich viele solcher Impulse gibt, die in die gleiche Richtung und zur gleichen Zeit gerichtet sind, kann eine Änderung der Neutrino-Flugrichtung signifikant sein. Und dies ist gerade den Fall, wenn sich ein Neutrino direkt einem rotierenden Quark eines Atoms der Materie nähert.
Durch die hohe Geschwindigkeit vor dem Neutrino bildet sich ein verdichtetes Vakuum. Das Neutrino trägt also eine dichte „Druckwelle“ vor sich (Abb. 39).
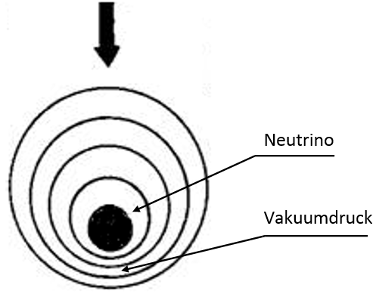
Abbildung 39: Erhöhte Vakuumdichte vor dem Neutrino
Jetzt stellen wir uns vor, dass dieses Neutrino beim Durchqueren der atomaren Hülle direkt zum Quark fliegt.
Ein Quark dreht sich mit größerer Geschwindigkeit (4,76 ⋅ 𝟏𝟎𝟖 𝒔^−𝟏) und bildet um sich herum ein verdichtetes rotierendes Vakuum. Je näher sich der Gluonen-Fluss zum Quark befindet, desto größere Geschwindigkeit und die Flussdichte hat er.
Zwei Teilchen, die gleiche Massen, aber unterschiedliche Art der Bewegungen haben, nähern sich zueinander. Das Neutrino, die sich eine verdichtete Druckwelle vorne trägt, tritt in die rotierenden verdichteten Schichten des Quarks. Da diese zwei Strömungen im rechten Winkel zueinander gerichtet sind, werden die oben genannten Kräfte (F) entstehen, die zur Abstoßung dieser Teilchen voneinander führt (Abb.40).
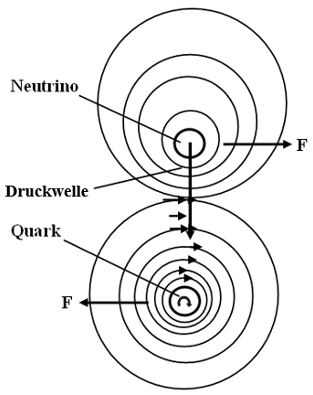
Abbildung 40: Der verdichtete gerichtete Fluss von Atomgluonen lenkt den Neutrino-Flugweg sofort ab
Diese verdichteten Gluonen-Ströme, die sich in einem Winkel zueinander bewegen, erzeugen eine Gegenkraft, die, durch die gegenseitige Abweichung der Teilchen, ihre Kollision verhindert. Dank dieses Mechanismus werden auch Kollisionen zwischen Neutrinos vermieden, die aufeinander zu oder in einem Winkel zueinander fliegen.
Ein "ähnliches" Phänomen kann in der Natur beobachtet werden, als eine im Regen fliegende Mücke durch den vor dem fallenden Tropfen gebildeten Druckluftstrom abgelenkt wird und somit trocken bleibt.
Wieso kommt es ab und zu doch zur Kollision?
Wie wir wissen, eine kinetische Energie hängt von der Masse und der Geschwindigkeit des fliegenden Teilchen (𝑬𝒌𝒊𝒏 = 𝟏/𝟐 ⋅ 𝒎𝞾𝟐) ab.
Da die Masse des Neutrinos einen konstanten Wert von m = 4,19· 10^−31 kg hat, hängt die kinetische Energie des Neutrinos nur von der Geschwindigkeit seiner Bewegung im Universum ab.
Astrophysiker haben schon eine große Anzahl von Neutrinos mit hoher und extrem hoher Energie registriert (mehr als 1 Peta-Elektronenvolt). Und das bedeutet, dass einige Neutrinos die Geschwindigkeiten haben, die viel höher sind, als die Lichtgeschwindigkeit.
Wie wir bereits wissen, haben die Geschwindigkeiten der chaotischen Bewegungen der Gluonen einen konstanten Wert (Lichtgeschwindigkeit).
Wenn das Neutrino schneller als mit der Lichtgeschwindigkeit fliegt, verkürzt sich die Zeit, die es benötigt, um durch das Atom zu fliegen. Da der verdichteten rotierenden Fluss von Gluonen eines Atoms, der senkrecht zum Flug der Neutrinos und ausschließlich von einer Seite gerichtet ist, konstant bleibt, aber die Zeit der Exposition gegenüber Neutrinos abnimmt, nimmt auch der insgesamt resultierende gepulste Effekt auf Neutrinos ab. Dies kann zu einer unzureichenden Abweichung des Neutrino-Flugweges führen, was manchmal zu einer Kollision mit dem Atomkern (Quarks) führt.
Zusammenfassung:
Mehr als 95 % unseres Universums bestehen aus dem Vakuum, das wiederum aus den absolut elastischen Mikroteilchen Gluonen besteht. Die Gluonen befinden sich in ständigen chaotischen Bewegungen. Da die Gluonen die kleinsten Teilchen im Universum sind, gibt es keine andere Substanz zwischen ihnen, durch die irgendwelche Wechselwirkungen übertragen werden könnten. Und das bedeutet, dass Gluonen keine Trägheit haben und, dementsprechend, keine kinetische Energie besitzen.
In der Anfangsphase des Universums hatten die Gluonen ihre eigene Geschwindigkeit und damit die individuelle Impulse (𝝆 = 𝒎𝞾).
Infolge der Kollisionen, prallten die Gluonen augenblicklich ab und teilten ihre Geschwindigkeiten gleichmäßig. Diese kontinuierliche Aufteilung der Geschwindigkeiten hat zu einem allmählichen Ausgleich der Energieimpulse aller Gluonen geführt. Und die daraus resultierende konstante Geschwindigkeit der Gluonen wurde als Lichtgeschwindigkeit (c) bekannt.
Somit übertragen Gluonen die Informationen in Form von Photonen nicht aufgrund der Größe der Energie eines einzelnen Impulses (da sie unverändert bleiben), sondern aufgrund ihrer Wiederholungsrate.
Diese Gluonen spielen, neben der Übertragung der elektromagnetischen Wellen (Photonen), eine entscheidende Rolle bei der Entstehung von Materie.
Ein Proton besteht aus rotierenden Up-Quark und Down-Quark, die die Wirbelströmungen des Vakuums erzeugen. Dank ihrer Zusammenwirkung, wird eine verdichtete stabile und elastische Hülle gebildet.
Bei der Kernfusion zwischen den vier Protonen, werden neben den drei Neutrinos und die Gammastrahlung, ein Atom des Heliums entstanden. Durch die weiteren Zusammenwirkungen Helium Atomen und Wasserstoff Atomen miteinander werden sich andere Atome und Moleküle der verschiedenen Stoffe herausgebildet.
Infolge der Kernfusionen, die im Inneren der Sterne ständig stattfinden, entstehen Neutrinos, die in allen Richtungen durch das All rasen.
Jedes Neutrino, das durch das Atom fliegt, erzeugt eine Zugkraft, die auf das Atom ausübt und verliert dabei einen winzigen Teil seiner kinetischen Energie. Diese Zugkraft des Neutrinos, die im Atom geblieben ist, heißt die Gravitationskraft des Neutrinos. Die resultierende vektorielle Kraft von allen Gravitationskräften der Neutrinos, die momentan durch das Atom fliegen, gibt dem Atom seine Gravitation 𝑭𝑮.
Jeder Himmelskörper im Universum wird von allen Seiten mit den riesigen Zahlen von Neutrinos bombardiert. Die Neutrino-Zahldichte und ihre kinetischen Energien, die von jeder Seite des Universums ankommen, sind ungleich.
Diese Zahldichte und Stärke der Neutrinos hängen von dem Ort des Kosmos ab, aus welchem diese Neutrinos abgestrahlt wurden.
Je man näher sich zum Zentrum des Universums befindet, desto höher ist die Dichte (Anzahl) der Sterne und umgekehrt, je man weiter sich vom Zentrum in die Richtung der Peripherie des Kosmos entfernen wird, desto geringer sind die Dichte der Sterne und damit die Dichte der Neutrinos.
Es führt dazu, dass die resultierende vektorielle Kraft, die ständig auf den Körper einwirkt, in die Richtung der Peripherie des Kosmos gesteuert wird. Diese Kraft treibt jeder Körper mit der Beschleunigung in diese Richtung hinaus.
So dehnt sich unser Universum aus!
Infolge des Schatteneffektes, der immer zwischen nahe beieinander liegenden Körpern stattfindet, entstehen Gravitationskräfte, die die Körper zueinander drücken. Diese Kräfte definieren die Umlaufbahnen aller Planeten, Kometen und Satelliten in unserem Sonnensystem sowie die Bewegungen von Sternen und Galaxien im gesamten Universum.