Teil 1
Die Grundlage des materiellen Universums
Wenn wir ein Mikroskop hätten, mit dem wir immer tiefer in die Struktur der Materie eintauchen können, würden wir Folgendes sehen:
-Zuerst würden wir ein Molekül sehen (Größe ≈ 1•10^-10 m).
-Dann die Atome, aus denen das Molekül besteht (Größe ≈ 1•10^-11 m).
-Bei dem Blick ins Innere des Atoms würden wir die Quark-Teilchen sehen (Durchmesser = 1•10^-16 m).
-Schauen wir noch tiefer in die verdichtete Schale, die sich um das Quark dreht, würden wir die Gluonen sehen (Durchmesser = 1•10^-24 m), die diese Schale aufbauen.
Ein noch kleineres Teilchen gibt es nicht.
Kapitel 1
Mechanik der Mikroteilchen
Versuchen wir unsere materielle Welt in umgekehrter Reihenfolge zu betrachten – beginnend mit der Leere. Die Leere ist ein bestimmtes Volumen im Raum, in dem sich kein Materieteilchen befindet.
Um besser zu verstehen, wie sich die Ereignisse in dieser Leere weiterentwickeln, stellen wir uns vor, dass unser Universum eine hohle Kugel ist, die aus absolut elastischem Material besteht. Die Elastizität des Materials hat zu Folge, dass bei gegenseitiger Kollision zweier absolut elastischer Partikel keine Deformation der Kugel stattfindet und somit kein Energieverlust entsteht, welcher für diese Deformation von Partikeln aufgewendet würde. Daher kann die gesamte in der Kugel (unserem Universum) enthaltene Energie nicht über ihre Grenzen hinausgehen.
Es ist bekannt, dass ein System ohne Interaktion mit der äußeren Umgebung (wie in unserem isolierten Bereich) abgeschlossenes System genannt wird. Somit bleibt die gesamte Energie in diesem System unverändert und kann nur von einer Energieart auf eine andere übertragen werden.
Am Anfang ist unser Raum, in dem wir versuchen werden, unser Universum zu bauen, absolut leer und jede Rede von irgendeiner Energie in unserem leeren Raum wäre absurd. Wir wissen, dass es keine Energie ohne Masse und Geschwindigkeit gibt.
Deshalb brauchen wir das erste materielle Teilchen, das das kleinste und zahlreichste Teilchen des Universums sein sollte.
Diese Rolle des ersten kleinsten Teilchens des Universums könnte theoretisch das Gluon Teilchen spielen, das uns aus der modernen Elementarteilchenphysik schon bekannt ist.
Dieses Teilchen muss ein absolut elastisches Teilchen sein, dessen Durchmesser, basierend auf der funktionalen Logik 1•10^-24 m nicht überschreiten darf.
An dieser Stelle möchte ich die Aussage machen, daß alle Größen der Teilchen, die später in unsere Theorie einbezogen werden, natürlich von den von uns akzeptierten Größen abweichen können. Aber diese natürlich möglichen Ungenauigkeiten können die Konstruktionsprinzipien unserer Theorie nicht wesentlich beeinflussen.
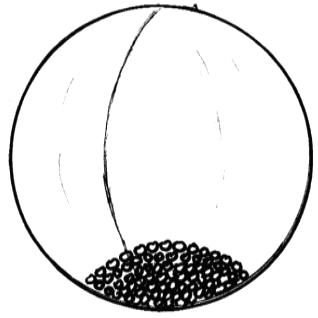
Abbildung 1: Absolut elastische Kugel mit den Gluonen ohne Energie
In der Kugel befinden sich Gluonen in absoluter Leere, jedoch ohne Bewegung. Um nun eine große Menge Energie in der Kugel zu erzeugen, stellen wir uns vor, diese kräftig zu schütteln, sodass alle Partikel in eine chaotische Bewegung versetzt werden (Abb. 2).

Abbildung 2: Absolut elastische Kugel und die Gluonen nach der Energieaufnahme
Da die Gluonen die ersten und kleinsten Teilchen unseres Universums sind, gibt es zwischen ihnen keine andere Substanz, durch die sie in irgendeiner Weise interagieren können, außer durch direkte Kollisionen miteinander.
Somit gibt es auf dieser Ebene des Universums noch keine Trägheitskräfte und folglich haben die Gluonpartikel keine Trägheit.
Es scheint, dass wir in drei Jahrhunderten der Entwicklung der Physik alles über Trägheit wissen. Die Trägheit ist die Eigenschaft eines materiellen Körpers, einen Zustand der Ruhe oder einer gleichmäßigen geradlinigen Bewegung aufrechtzuerhalten, bis eine äußere Kraft diesen Zustand verändert.
Aber was gibt uns das Wort „Eigenschaft“ oder „Fähigkeit“ des Körpers, diesen oder jenen Zustand aufrechtzuerhalten? Dies ist nur die Feststellung der Tatsache, dass es unbegreifliche Kräfte gibt.
Die physikalische Natur solcher Trägheitskräfte lässt sich mit Hilfe der modernen Theorie der Quantenphysik nicht erklären.
Die Analyse der Trägheitsgesetze zeigt, dass es zwei grundlegende physikalische Eigenschaften von Körpern bzw. zwei Arten mechanischer Trägheit gibt: die Trägheit der Ruhe und die Trägheit der Bewegung.
Zunächst zeigt ein Körper Trägheit, indem er sich einer Veränderung seines Bewegungszustands widersetzt – also etwa der Versetzung aus dem Ruhezustand in Bewegung. Sobald sich der Körper bewegt, widersetzt er sich wiederum jeder äußeren Einwirkung, die seine Geschwindigkeit verändern möchte – sei es eine Beschleunigung, Verzögerung oder ein vollständiger Stopp.
Was bedeutet es, einem Einfluss zu widerstehen?
Mechanisch zu widerstehen bedeutet, sich an etwas „festzuhalten“. Wenn uns jemand von unserem Platz wegbewegen möchte, wir uns aber an nichts festhalten können, gelingt ihm dies unabhängig davon, ob wir unsere Muskelkraft einsetzen oder nicht. Wäre es so einfach, hätte sich „Baron Münchhausen“ tatsächlich samt Pferd am eigenen Schopf aus dem Sumpf ziehen können – nur durch reine Willensanstrengung.
Schon Aristoteles sagte im 8. Jahrhundert v. Chr.: „Alles, was sich bewegt, bewegt sich aufgrund des Einflusses eines anderen Körpers.“
Daraus lässt sich schließen:
Damit ein materielles Teilchen Trägheit zeigen kann, muss mindestens eine weitere materielle Substanz vorhanden sein, mit der es wechselwirkt.
Was Trägheit ist und wie sie entsteht, wurde bereits auf Seite 18 ausführlich erklärt. An dieser Stelle sei nur noch ergänzt: Trägheit entsteht durch die Wechselwirkung von Gluonen mit anderen Teilchen, die sich bewegen oder in Bewegung versetzt werden.
Daraus folgt:
Alle materiellen Teilchen und Substanzen besitzen Trägheit – mit Ausnahme der Gluonen selbst.
Diese Abwesenheit der Trägheit bei Gluonen ist die Haupttatsache, auf der die gesamte Theorie der Entstehung der Materie des Universums aufgebaut sein wird.
Da unsere Gluonen keine Trägheit haben, haben sie auch keine kinetische Energie. Infolgedessen tragen Gluonen nur einen Impulsvektor in sich, wenn sie sich bewegen.
Der Impuls oder auch die Energiemenge eines Materialpunkts kann als Vektor verstanden werden, der dem Produkt der Masse des Materialpunkts mit seinem Geschwindigkeitsvektor entspricht: (𝒑'⃗ = 𝒎𝑽'⃗) P = mV
Aufgrund gewisser Schreibschwierigkeiten werden die Vektorsymbole in allen weiteren Formeln fehlen!
Der anfängliche Energiestoß bewirkt, dass sich die Teilchen chaotisch bewegen. Als Ergebnis teilen alle Teilchen, die ständig miteinander kollidieren, ihre Impulse untereinander auf nach: m1 V1 + m2 V2 = m1 U1 + m2 U2
Bei einem zentralen (frontalen) Aufprall von zwei Partikeln werden ihre Geschwindigkeiten vor und nach der Kollision entlang einer geraden Linie gerichtet.
Da die Gluonen keine kinetische Energie besitzen und ihre Massen gleich sind, verteilen sich ihre Vektorimpulse wie in Abb. 3 dargestellt:
P = P 1 + P 2 = m1 V1 + m2 V2 = m1 U1 + m2 U2 da m1 = m2 V1 + V2 = U1 + U2
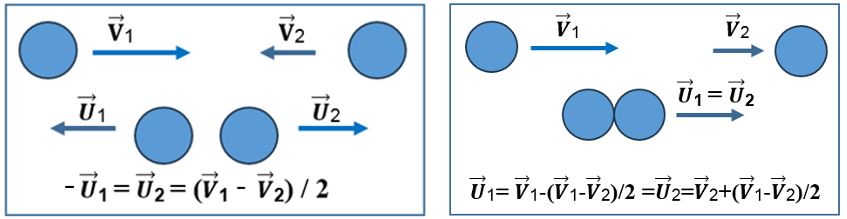
Abbildung 3: Verteilung der Geschwindigkeiten nach zentralem Aufprall von zwei Gluonen
Da es zwischen den Gluonpartikeln keine andere Substanz als die Leere gibt, gibt es keinen Unterschied (nach dem Relativitätsgesetz), welches Partikel und mit welcher Geschwindigkeit auf ein anderes Partikel zu flog. Entscheidend ist nur die Annäherungsgeschwindigkeit der Teilchen vor dem Aufprall.
Es muss auch darauf geachtet werden, dass die Zeit der Umverteilung von Impulsen bei einer Kollision von Gluonen gleich Null ist. Dies geht von der Tatsache aus, dass Gluonen absolut elastische Teilchen sind und dabei keine Trägheit besitzen, was bedeutet, dass sie keine kinetische Energie in sich tragen, wenn sie sich bewegen.
Erinnern Sie sich an die Tatsache, dass wenn die Geschwindigkeitsvektoren aufeinander gerichtet sind, ihre Werte entgegengesetzte Vorzeichen haben (Vektor V1 = 10; Vektor V2 = -6).
Vektoren - U1 = U2 = {10 - (-6)} / 2 = 16 / 2 = 8 Vektor U1 = - 8 Vektor U2 = 8
Zentrale Kollisionen zwischen den Gluonen passieren sehr selten vor.
Meistens sind die Teilchengeschwindigkeiten vor einer Kollision in einem bestimmten Winkel zueinander gerichtet.
Zur Verdeutlichung habe ich ein Beispiel (Abb. 4) für eine außermittige Kollision zweier Gluonen mit unterschiedlichen Geschwindigkeiten gegeben, das eine grafische Definition der Richtung ihrer Reflexionen und ihrer Geschwindigkeitswerte zeigt.
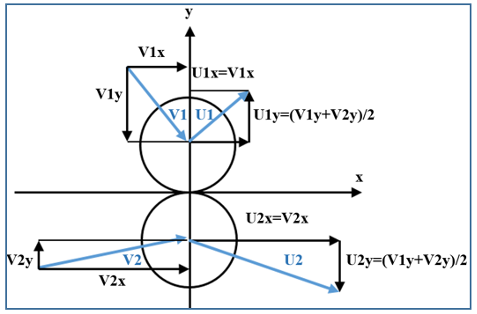
Abbildung 4: Grafische Bestimmung der Reflexionsparameter zweier Gluonen
Die Umverteilung der Geschwindigkeiten nach dem Aufprall der Partikel erfolgt in diesem Fall nicht zwischen den absoluten Geschwindigkeiten beider Partikel V1 und V2, sondern nur zwischen den Annäherungsgeschwindigkeiten der Partikel V1y und V2y (Projektionen der Geschwindigkeiten V1 und V2 auf die y-Achse) zueinander.
Die Geschwindigkeiten V1x und V2x (Projektionen der Geschwindigkeiten V1 und V2 auf der x-Achse) bleiben unverändert.
Betrachten wir nun, wozu diese chaotischen Bewegungen der Gluonen im Universum führen werden.
Je größer die Anzahl der Teilchen (N) und deren mittlere Geschwindigkeit (υ) der chaotischen Bewegung im entsprechenden Volumen (V) sind, desto weniger Zeit benötigen die Teilchen vor ihrer nächsten Kollision.
Chaotische Bewegungen der Teilchen, ihre Impulse (P = m υ) und damit ihre Geschwindigkeiten mit der Zeit gleichen sich aus.
Wenn die Geschwindigkeiten aller Gluonen nach einer bestimmten Zeit gleich sind, sind auch die Abstände zwischen den Teilchen gleich.
All dies führt dazu, dass die Dichte 𝝆𝟎 der Gluonen und damit der Druck 𝑷𝟎 im Raum ausgeglichen sind.
Dieser Raum wird als ausgeglichener Raum oder Vakuum bezeichnet.
Für die weitere Wahrnehmung der Prozesse ist es wichtig, diese beiden Begriffe (Druck und Dichte) genau zu verstehen.
Die Dichte der Gluonen in einem bestimmten Volumen beträgt:
𝝆𝟎 = 𝒎𝟎 •𝑵/𝑽
Hier sind:
𝑷𝟎 - Der Druck der Gluonen in einem ausgeglichenen Raum [Pa].
𝝆𝟎 - Die Dichte der Gluonen im ausgeglichenen Raum [kg m^-3].
𝒎𝟎 - Die Masse des Gluons [kg].
𝑵 - Die Anzahl der Gluonen in einem bestimmten Volumen.
𝑽 - Ein definiertes Volumen [m3].
υ - Die chaotische Geschwindigkeit der Gluonen [m s^-1].
Unter der Partikeldichte 𝝆𝟎 und in unserem Fall unter der Dichte der Gluonen 𝑷𝟎 versteht man also die Summe aller Gluonen, die sich in einem bestimmten Vakuumvolumen (m^3) befinden. Da in einem ausgeglichenen Raum die Abstände zwischen den Teilchen ungefähr gleich sind, sagt uns die Dichte, wie weit die Teilchen zueinander liegen. Dabei dürfen wir nicht vergessen, dass sich alle Teilchen in ständiger chaotischer Bewegung innerhalb dieser Entfernungen befinden, kollidieren und ihre Impulse austauschen.
Der Druck der Gluonen 𝑷𝟎 im ausgeglichenen Raum ist aus der Abb. 5 verdeutlicht.
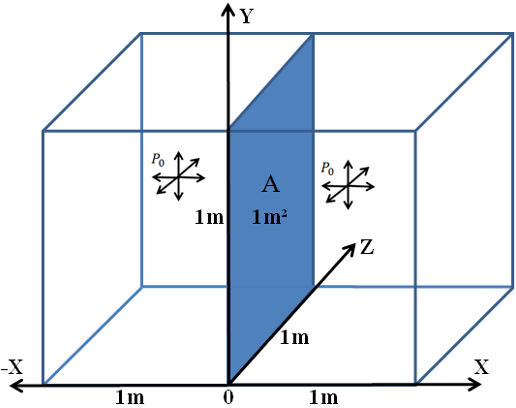
Abbildung 5: Entstehung des Druckes 𝑷𝟎 im ausgeglichenen Raum
Wenn wir eine quadratische Fläche (A) mit den Seiten von 1m in der Mitte des Raums darstellen, werden die beiden Seiten der Fläche dem Beschuss der Gluonen ausgesetzt.
Es ist bekannt, dass der Druck 𝑷 das Ergebnis der Kraft F senkrecht zur Oberfläche A ist:
𝑷 = 𝑭 / 𝐀 [𝒌𝒈𝒎/𝒔^𝟐𝒎^𝟐]
Die Gesamtzahl der im rechten Kubikmeter Raum befindlichen Gluonen (N) stimmt mit der Anzahl der Gluonen im linken Volumen (1 m^3) überein.
Jeder Kubikmeter des Raumes hat für die Gluonen sechs freie Bewegungsrichtungen entlang der Koordinatenachsen: x; y; z; -x; -y; -z.
Da die chaotischen Bewegungen der Partikel ausbalanciert sind, nimmt jede der Seiten des Volumens durchschnittlich ein Sechstel aller angreifenden Partikel (1/6 N) wahr. Die mittlere quadratische Fläche (A) nimmt einerseits ein Sechstel aller Gluonen dieser Seite wahr.
Die andere Seite der Oberfläche (A) erhält gleichzeitig die gleiche Anzahl Gluonen (1/6 N).
Auf diese Weise erfährt die Fläche (A) auf beiden Seiten insgesamt 1/3 N Schläge der Gluonen mit einer Gesamtmasse an Teilchen von 𝒎 = 𝟏/3 𝒎𝟎 •𝑵.
𝑷 = 𝑭 / 𝐀 = 𝑬 / 𝐕 = 𝒎𝝊^𝟐 / 𝐕 = 𝟏/3 𝒎𝟎 •𝑵• 𝝊^𝟐 / 𝐕
Insolange 𝝆𝟎 = 𝒎𝟎 •𝑵 / 𝐕
𝑷𝟎 =𝟏/3𝝆𝟎 • 𝝊^𝟐
Also, der Druck wird durch die Schläge der Gluonen auf den Körper im Vakuum verursacht. Mit anderen Worten, die Anzahl der Schläge von Gluonen, die zu jeder Zeit auf jede minimale Körperoberfläche fallen, wird praktisch gleich sein. Der gleiche Druck in allen Richtungen ist das Ergebnis der ungeordneten Bewegung einer großen Anzahl von Teilchen. Dieser Druck hängt direkt proportional von der Anzahl dieser Teilchen in einem bestimmten Volumen und damit von der Dichte des Vakuums ab.
Je höher die Dichte, desto höher der Druck!
Wie groß die Werte der Geschwindigkeiten der Gluonen, wie ihre Dichte und Druck letztendlich in einem ausgeglichenen Universum entstehen werden, hängt vom Volumen des gesamten Raums, der Gesamtzahl der Gluonen und der in Gluonen eingesetzten Gesamtenergie ab.
Da die Schaffung unseres Universums ein einzigartiges, einmaliges Ereignis war, wurden all jene Werte einmal vergeben und bleiben konstant.
Daher werden in unserem ausgewogenen und etablierten Universum (d.h. im Vakuum) die Geschwindigkeiten der chaotischen Bewegungen der Gluonen, ihre Dichte und ihr Druck ebenfalls konstante Werte haben.
Die Geschwindigkeit, bei der die chaotische Bewegung der Gluonen auftritt, wurde schon vor langer Zeit gemessen und als Lichtgeschwindigkeit (im Vakuum) bezeichnet: c=2,99792458·10^8m/s
Somit sieht die endgültige Formel für den Druck, die Dichte und die Geschwindigkeit der Gluonen nun so aus:
𝑷𝟎 =1/3𝝆𝟎 c^2
Alle mit Lichtgeschwindigkeit fliegenden Gluonen, die miteinander kollidieren, ihre Impulse austauschen und ihre Bewegungsrichtung ändern, werden als Gluonen-Substanz bezeichnet.
Ein Raum, in dem sich nur die Gluonen-Substanz befindet, wird als Vakuum bezeichnet.
Somit ist das Vakuum kein leerer Raum. Das Vakuum ist frei von Atomen und Molekülen, aber nicht von Gluonen.
Fassen wir die Eigenschaften des Vakuums zusammen:
- Das Vakuum ist der erste von zwei Bestandteilen des materiellen Universums und besteht aus Mikropartikeln (Gluonen), die das gesamte Universum ausfüllen.
- Gluonen sind absolut elastische Teilchen mit einem Durchmesser von 1 · 10^-24 m.
- Teilchen, die der Wirkung der Schwerkraft und Trägheit nicht ausgesetzt sind, bewegen sich chaotisch mit Lichtgeschwindigkeit in einem begrenzten Radius (bis zu ihrem nächsten Zusammenstoß).
- Da die Massen der Gluonen und ihre Geschwindigkeiten gleich sind, verändern sich nach den Kollisionen nur ihre vektorielle Reflexionsrichtungen.
- Die Gluonen selbst fliegen nicht über weite Strecken, sondern sind aufgrund ständiger Kollisionen in einem oszillierenden Prozess, limitiert auf einen begrenzten Radius.
- Ihre Impulse, infolge der ständigen Kollisionen der Gluonen untereinander, werden mit der Lichtgeschwindigkeit in alle Richtungen übertragen.
- Die Gluonen sind Vermittler von Informationen, dessen Informationsdichte durch die Häufigkeit aufeinander folgender Kollisionen bestimmt wird, (siehe folgende Kapitel).
- Da die Gluonen absolut elastische Partikel sind, treten ihre Kollisionen verzögerungsfrei auf. Weil die Zeit der übertragenen Kollisionen gleich Null ist, muss auch die Impulsübertragungszeit gleich null sein.
Bisher beschrieben wir den Raum ohne Fremdkörper. Ein solcher Raum, der nur aus Gluonen (d.h. Gluonensubstanz) besteht, nennen wir Vakuum.
Das Vakuum ist ein Teil des Universums und macht mehr als 95 % unseres Weltalls aus.
Ein Universum, das nur aus Vakuum besteht, wäre sehr langweilig. Es ist eintönig. Der Druck, die Dichte und die Geschwindigkeit der Gluonen sind im gesamten Weltraum gleich. Vergessen wir nicht, dass das gesamte Vakuum des Universums mit enormer Energie gefüllt ist, die aus der Summe aller Energien des Gluonenimpulses besteht: E = pc
Da (p = mc) E = mc^2
E - ist die Gesamtenergie des Universums.
m - ist die Gesamtmasse aller Gluonen im Universum.
p - ist die Summe aller Gluonenimpulse des Universums.
c - ist die mittlere Bewegungsgeschwindigkeit der Gluonen im Vakuum.
Bis jetzt gibt es in diesem Vakuum keine materielle Komponente in Form von Planeten, Sternen, Galaxien und allem was uns vertraut ist.
Für ihre Entstehung benötigen wir ein zweites, absolut elastisches Teilchen, dessen Rolle ein bereits bekanntes Teilchen des Quarks spielen kann.
Die Größe eines Quarkteilchens ist viel größer als die Größe eines Gluons. Das Verhältnis zwischen den beiden Teilchen kann mit einem Basketball zu einem Luftmolekül verglichen werden.
Die Anzahl der Quarks im Universum ist sehr groß, aber erheblich kleiner als die Zahl der Gluonen.
Jetzt brauchen wir wieder einen Schöpfer, der alle Quark-Partikel in unser ausgeglichenes Vakuum bringt.
Als Nächstes konzentrieren wir uns auf den Prozess des gegenseitigen Einflusses von Quarks und Gluonen.
Was passiert mit einem Quark, das in die Gluonen-Masse des etablierten Vakuums gebracht wird?
Jedes Quark ist natürlich von allen Seiten Angriffen von Gluonen ausgesetzt. Da Druck und Dichte der Gluonen im stationären Vakuum konstante Werte sind, wird die Anzahl der Kollisionen von Gluonen mit einem Quark von allen Seiten gleich sein. Das bedeutet, dass die Resultante aller Impulskollisionen annähernd Null ist. Wenn das Quark also eine vollkommen glatte, kugelförmige Oberfläche hätte, würde ihm so gut wie nichts passieren und es würde ohne Bewegung an seinem Platz geblieben.
Bei einem solch passiven Zustand der Quarks ist von der Bildung von Atomen keine Rede.
Damit zwischen den Quarks bestimmte Bedingungen für ihre gegenseitige Beeinflussung mit anschließender Bildung der Atome entstehen, müssen alle Quarks in Rotationsbewegung gebracht werden.
Nur kolossale Rotationen der Quarks, mit der Beteiligung von Gluonen an dieser Rotation, können eine Bedingung schaffen, unter der es in diesem begrenzten Bereich des Vakuums zu einer Druckabnahme kommt.
Dieser Druckunterschied, der in den Regionen der rotierenden Quarks (P) und des freien ausgeglichenen Vakuums entsteht, ist die Hauptvoraussetzung für die Entstehung der Atome.
Es sei darauf hingewiesen, dass jedes chemische Element, sei es Wasserstoff, Helium oder Gold, eine genau definierte Struktur, physikalische Eigenschaften und Parameter hat. Und da alle diese Elemente in ihrer Basis aus Quarks bestehen, ist diese Homogenität identischer Stoffe nur möglich, wenn die Form aller Quarks und ihre Drehgeschwindigkeiten gleich und relativ stabil sind.
Was könnte Quarks dazu bringen, im Vakuum zu rotieren, und zwar mit der gleichen Winkelgeschwindigkeit?
Als eine der möglichen Optionen würde ich es wagen, eine bestimmte Form von Quarkteilchen vorzuschlagen, mit der alle oben genannten Anforderungen erfüllt werden könnten, und dies anhand von Abbildung 6 zu erläutern.
Die Außenseite eines jeden Quarks hat keine vollkommen glatte Oberfläche. Etwa 1/24 der gesamten Oberfläche eines Quarks besteht aus kleinen Ausstülpungen, die in ihrer Form einem Viertel einer Kugel entsprechen, die, sagen wir, in drei Reihen entlang der Äquatoriallinie des Quarks angeordnet und streng in eine bestimmte Richtung gerichtet sind.
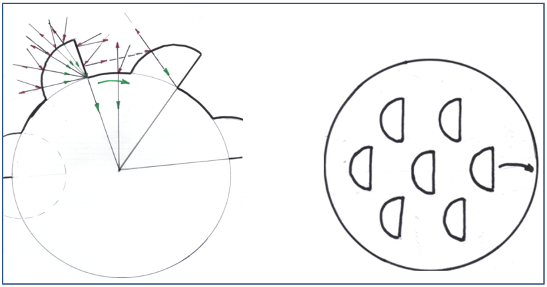
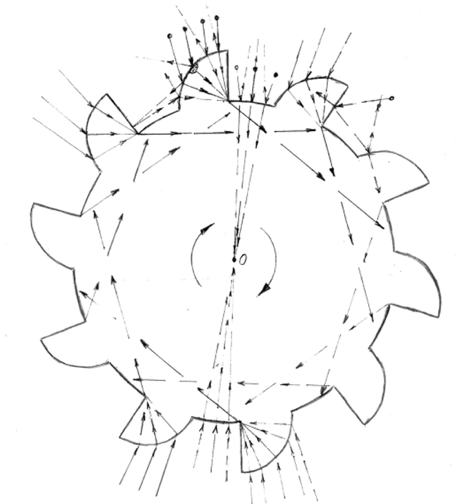
Abbildung 6: 1/24 der gesamten Oberfläche eines Quarks besteht aus kleinen Ausstülpungen
Die Größe der Ausstülpung ist in Wirklichkeit um ein Vielfaches kleiner als die Größe des Quarks selbst und entspricht keineswegs unserer Zeichnung. Dies haben wir nur zur Verdeutlichung des Geschehensablaufes gezeigt.
Aufgrund der Berechnungen, logischer und funktioneller Rollen der Ausstülpungen des Quarks, wage ich anzunehmen, dass der Radius der Ausstülpungen rAqu = 1·10^-19 m ist.
Wenn wir den Radius der Ausstülpungen kennen, können wir deren Masse auch bestimmen.
Das Volumen der Wölbung, das 1/4 der Kugel ist, wird durch die Formel berechnet:
VAqu = 1/4·4/3·nr^3 = 1/4·4/3·3,14·(1·10^-19)^3 = 1,047·10^-57 m^3
Einige Physiker behaupten, dass die ungefähre Dichte von Atomkernen p = 8·10^17 kg/m^3 betragen, was der Dichte eines Neutronensterns entspricht. Unsere Teilchendichten würden mindestens die gleiche Größenordnung haben.
https://www.cosmos-indirekt.de//Physik-Schule/Neutronenstern
Da die Dichte des Quarks 8·10^17 kg/m^3 ist, berechnen wir gleich die Masse des Gluons, die Masse des Quarks und die Masse der Ausstülpung des Quarks:
Vgl = 4/3·nrgl^3 = 4/3·3,14·(5·10^-25)^3 = 5,236·10^-73 m^3
Vqu = 4/3·nrqu^3 = 4/3·3,14·(5·10^-17)^3 = 5,236·10^-49 m^3
mgl = p·Vgl = 8·10^17·5,236·10^-73 = 4,19·10^-55 kg
mqu = p·Vgu = 8·10^17·5,236·10^-49 = 4,19·10^-31 kg
mAqu = p·VAqu = 8·10^17·1,047·10^-57 = 8,376·10^-40 kg
Alle Vektorimpulse von Gluonen (p = m𝝊) die auf die Oberfläche der Konvexität fallen, werden gemäß dem Impulserhaltungsgesetz umverteilt. Die Reflexionsrichtungen der Impulse voneinander werden senkrecht zu diesen Kontaktflächen gerichtet. Aufgrund der Tatsache, dass die Ausstülpung des Quarks die Form eines Teils der Kugel hat, werden die Reflexionsimpulse entlang der Richtung des Centers der kleinen Kugel gerichtet.
Somit werden alle von Gluonen reflektierten Impulsvektoren auf einen Punkt des konvexen Zentrums gerichtet, wodurch ein Drehmoment für das gesamte Quark erzeugt wird. Da es viele solcher Ausstülpungen gibt und sie alle in eine Richtung gerichtet sind, addieren sich ihre Drehmomente. Infolgedessen beginnt sich der Quark mit der Beschleunigung zu drehen. Die Erhöhung der Drehzahl setzt sich fort, bis die fortschreitende lineare Geschwindigkeit der Ausstülpung des Quarks (𝝊Aqu) einen bestimmten Wert erreicht.
Dies wird geschehen, wenn der Impuls des Gluons und entgegen liegenden Impulses der Ausstülpungen des Quarks die Gleichheit erreichen wird:
mgl·cgl = mAqu·𝝊Aqu
Nun bestimmen wir die Geschwindigkeit der Translationsbewegung der Ausstülpung des Quarks:
𝝊Aqu = mgl·cgl /mAqu =4,19·10^-55 kg·2,99792458·10^8 m/s / 8,376·10^-40 kg = 1,5·10^-7 m/s
Da sich die Ausstülpungen auf der Oberfläche des Quarks befinden, nehmen ihre linearen Geschwindigkeiten die Richtung der Drehung des Quarks.
Wenn wir den Umfang des Quarks (Lqu) bestimmen, können wir dann die Zeit T berechnen, die eine Ausstülpung benötigt, um diese Länge (eine Umdrehung des Quarks) zu überwinden:
Lqu = 2πrqu = 2 · 3,14159 · 5 · 10^-17 m= 3,142 · 10^-16 m
Tqu = Lqu. / 𝝊Aqu = 3,142 · 3,142 · 10^-16 / 1,5 · 10^-7 =2,1 ·10^-9 s
Jetzt können wir die Anzahl der Umdrehungen bestimmen, die das Quark in einer Sekunde oder
Minute ausführt:
n = 1/T = 1 / 2,1 · 10^-9 = 4,76 · 10^8 s^-1 = 2,85 · 10^10 min^-1
Nun können wir uns die kolossale Winkelgeschwindigkeit vorstellen, mit der sich die Quarks drehen und wie viel Energie in dieser Drehung enthalten ist.
Da die Abmessungen der Ausstülpungen des Quarks 200.000-mal größer, als die Teilchengröße des Gluons sind, beeinflussen diese Bulges die Umverteilung der Vektorimpulsreflexionen der Gluonen von der rotierenden Oberfläche des Quarks erheblich. Dies führt dazu, dass die Quark- Partikel das zu Ihm benachbarte Vakuum in eine gemeinsame Rotation mitreißen wird (Abb. 7).
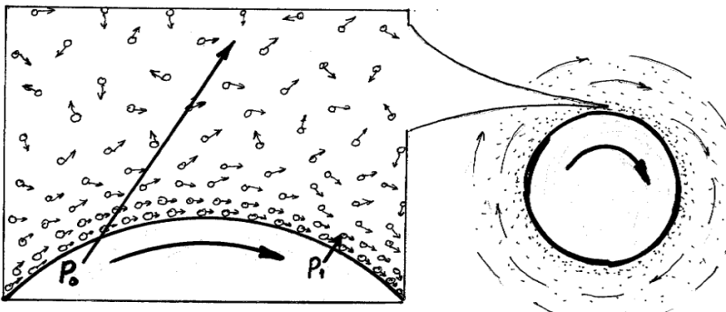
Abbildung 7: Rotierender Quark mit dem von ihm gebildeten drehenden Gluonen-Substanz
Ich möchte noch einmal daran erinnern, dass Gluonen die ersten und kleinsten Teilchen des Universums sind. Zwischen ihnen gibt es keine andere Substanz, durch die irgendwelche Wechselwirkungen übertragen werden könnten. Das wiederum bedeutet, dass Gluonen keine Trägheit besitzen und daher bei ihrer Rotation keinen Fliehkräften ausgesetzt sind und nicht vom Rotationszentrum wegfliegen. Jedes Gluon fliegt nach der Kollision mit einem anderen Gluon und nachdem es sofort einen neuen Impulsvektor erhalten hat, bis zur nächsten Kollision in einer geraden Linie weiter.
Bei Kollisionen von Gluonen mit den Ausbuchtungen des rotierenden Quarks werden die wahrscheinlichen Richtungen ihrer Reflexionen entlang der rotierenden Oberfläche des Quarks gerichtet sein. Dadurch sinkt der Vakuumdruck in der Nähe des Quarks, und die Zahl der angreifenden Gluonen, die senkrecht auf das Quark zufliegen, steigt. Dies führt dazu, dass die nahen fliegenden Gluonen näher an die Oberfläche des rotierenden Quarks gedrückt werden. Und all dies führt zu einer Erhöhung der Vakuumdichte. Diese Zunahme der Vakuumdichte um das Quark wird sich fortsetzen, bis die Winkelgeschwindigkeit der Rotation des Quarks ihren berechneten Wert von 4,76 · 10^8 s^-1 erreicht:
Diese kolossale Dichte des sich drehenden Vakuums nimmt allmählich ab, wenn man sich vom Rotationszentrum des Quarks entfernt.
Da alle Quarks die gleiche Struktur und Masse haben, drehen sie sich mit der gleichen Winkelgeschwindigkeit, aber die Drehrichtung kann natürlich unterschiedlich sein.Die Quarks, die sich in eine Richtung drehen (z. B. im Uhrzeigersinn), bezeichne ich als u-Quarks, die anderen als d-Quarks.
Infolge der Wechselwirkung zweier Quarks, die in leicht unterschiedlichen Ebenen rotieren, richten sich ihre Rotationsebenen aufgrund der Gluonenflüsse des Vakuums allmählich aus und passen sich einander an.
Da Quarks und Gluonen absolut elastische Teilchen sind, werden ihre Impulsvektoren gemäß dem Impulserhaltungsgesetz nach der bereits bekannten Formel umverteilt:
mgl · cgl.1 + mqu · 𝝊qu.1 = mgl · 𝝊gl.2 + mqu · 𝝊qu.2
Die Masse des Quarks und die Masse des Gluons vor und nach der Kollision bleiben unverändert. Die Geschwindigkeit des Gluons vor der Kollision entsprach der Lichtgeschwindigkeit.
Nun kommt ein wichtiger Punkt zum Verständnis, warum unser Universum unendlich lange und stabil existieren kann.
Alles in dieser Welt ist abhängig von den notwendigen Bedingungen für die Wechselwirkung zweier Arten von Partikeln untereinander. Wie wir später sehen werden, wurden als Ergebnis solcher Wechselwirkungen alle Atome und Moleküle einfacher und komplexer Substanzen gebildet. Alle Atome und Moleküle eines bestimmten Stoffes haben bekanntlich eine genau definierte Struktur, die Eigenschaft und die Parameter.
Und dies ist nur möglich, wenn die Parameter aller Quarks unverändert und relativ stabil bleiben. Daher müssen die Rotationsgeschwindigkeiten aller Quarks gleich sein und die linearen Geschwindigkeiten sollten nicht wesentlich von ihren ständigen Kollisionen mit Gluonen abhängig sein.
Eine andere Tatsache legt nahe, dass sich alle Moleküle einer bestimmten Substanz in genau definierten Abständen voneinander befinden. Und alle Moleküle bestehen aus Atomen, die wiederum, wie wir später sehen werden, aus Quarks und Gluonen bestehen. Daraus schließen wir, dass Quarks in einem Atom, die ständig auf eine kolossale Armee von Gluonen treffen, ihre linearen Bewegungsgeschwindigkeiten nicht wesentlich verändern können.
Und dies ist nur möglich, wenn die Gluonen-Impulse und Quarks-Impulse vor und nach den Kollisionen relativ unverändert bleiben:
mgl · c = mqu · 𝝊qu.
Wir wissen, dass die Geschwindigkeiten der Teilchen Vektorgrößen sind.
Dies bedeutet, dass zum Zeitpunkt der Kollision des Gluons mit dem Quark eine sofortige Umverteilung von Impulsen auftritt, bei der die absoluten Geschwindigkeiten der Partikel und damit ihre absoluten Impulse unverändert bleiben. Ändern sich nur die Richtungsvektoren der Partikeleflexion.
Wenn ein sich bewegender materieller Körper auf einer Seite eine größere Anzahl von Kollisionen mit Gluonen aufweist als auf der anderen Seite, werden die Vektorrichtungen aller Impulse aufsummiert. Der resultierende Impulsvektor wirkt auf den materiellen Körper und ändert seine Bewegungsrichtung.
Aus unserer Formel für die Impulserhaltung folgt, dass die Masse des Quarks und die Masse des Gluons in solchen Verhältnissen stehen, wie die Geschwindigkeit des Gluons sich auf die Geschwindigkeit des Quarks bezieht.
Da uns Lichtgeschwindigkeit, Masse des Quarks und Mase des Gluons bekannt sind, kann man jetzt die Reflexionsgeschwindigkeit des Quarks nach seiner frontalen Kollision mit einem Gluon bestimmen:
𝝆𝑔𝑙 = 𝒎𝑔𝑙 · 𝒄𝑔𝑙 = 𝟒,𝟏𝟗⋅𝟏𝟎^−𝟓𝟓 · 𝟐,𝟗𝟗𝟕𝟗𝟐𝟒𝟓𝟖 · 𝟏𝟎^𝟖 =𝟏,𝟐𝟔 · 𝟏𝟎^−𝟒𝟔 𝐤𝐠𝒎/s
𝛖𝒒𝒖 = 𝟏,𝟐𝟔 · 𝟏𝟎^−𝟒𝟔 / 4,19 · 10^-31 = 3 · 10^-16 m/s
Dies bedeutet, dass im Moment der Kollision eines mit der Lichtgeschwindigkeit fliegenden Gluonteilchens mit einem Quarkteilchen, das in einem Zustand minimaler linearer Annäherungsgeschwindigkeit befindet, Teilchen senkrecht zur Kontaktfläche reflektiert werden. Das Gluon wird mit der gleichen Lichtgeschwindigkeit reflektiert, und das Quark erhält einen Impuls 𝝆𝑔𝑙 = 𝟏,𝟐𝟔 · 𝟏𝟎^−𝟒𝟔 𝐤𝐠𝒎/s, der mit einer linearen Geschwindigkeit von 𝛖𝒒𝒖 = 3 · 10^-16 m/s auf das Zentrum des Teilchens gerichtet ist.
Wie wir sehen, ist die Translationsbewegung der rotierenden Quarks im Atom sehr unbedeutend. Und wenn wir die Tatsache berücksichtigen, dass das Quark von allen Seiten gleichzeitig mit Gluonen zusammenstößt, geht die resultierende Translationsbewegung des Quarks gegen Null.
Wir wissen, dass die Gluonen-Dichte und der Druck in einem ausgeglichenen Raum (im Vakuum) gemäß der Formel die konstante Werte sind.
Jetzt sind im Vakuum Quark-Partikel aufgetaucht, die beginnen, dieses hergestellte Gleichgewicht zu zerstören und ihre eigene Ordnung in ihre Umgebung einzuführen.
In diesem Fall treten in der Nähe von Quarks, die ihre Winkelgeschwindigkeiten oder linearen Verschiebungen ändern, Bedingungen auf, bei denen sich die Dichte und damit der Vakuumdruck (P) verändern.
Betrachten wir zunächst diejenigen Eigenschaften des Vakuums, die unter bestimmten Umständen den Wert der Dichte beeinflussen können.
1. Die Dichte des Vakuums Betrachten wir nun, was mit dem Druck des Vakuums geschieht, wenn plötzlich an irgendeinem Ort im Weltraum die Anzahl der Gluonen (ihre Dichte) sinkt.
Stellen wir uns ein Teilchen vor, das sich allmählich durch das Vakuum zu bewegen begann. Abbildungen 8 und 9 verdeutlichen diese Prozesse.
Im ersten Moment nimmt die Dichte des Vakuums hinter dem fliegenden Teilchen auf natürliche Weise ab, was an dieser Stelle zu einem Druckabfall im Verhältnis zum Außendruck des Vakuumsführt. Durch diese Druckdifferenz wird der leere Raum schnell mit Gluonen aus den äußeren Bereichen des Vakuums gefüllt. Dies wiederum führt zu einer Erhöhung der Dichte des Vakuums hinter den Partikeln.
Würde das Quark plötzlich stoppen, würde der Druck des Vakuums nach kurzer Zeit wieder ausgeglichen sein.
An dieser Stelle soll das Auftreten der Trägheit erläutert werden.
Erinnern wir uns an die Tatsache, dass ein Teilchen, das sich in einem ausgeglichenen Vakuum in Ruhe befindet, von allen Seiten die gleiche Anzahl von Kollisionen mit Gluonen erfährt. Jedes Gluon überträgt einen Impuls, so dass das Teilchen sofort die Richtung und die Geschwindigkeit der Bewegung im Raum entsprechend der gesamten momentanen Resultierenden aller Impulse ändert. Da die Gluonendichte um das unbewegliche Teilchen gleich ist, ist die Resultante aller Impulse gleich Null.
Stellen wir uns ein Teilchen vor, das eine Beschleunigung erfährt.
Vor dem fliegenden Teilchen wird die Dichte des Vakuums steigen, was zur Vergrößerung des Druckes führen wird (P2 > P0).
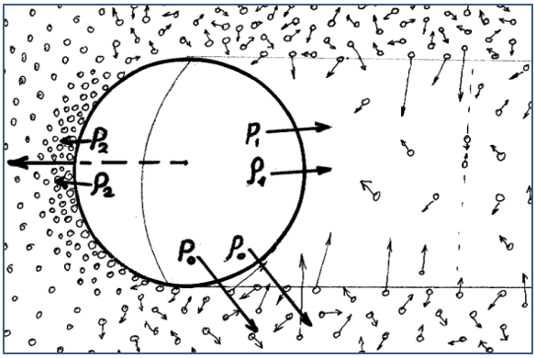
Abbildung 8: Ein Teilchen fängt an, mit einer Beschleunigung zu fliegen
Dieser erhöhte Druck wird in alle Richtungen und auch entgegen der Flugrichtung des Teilchens wirken, was zur Reduzierung der Geschwindigkeit des Teilchens führen wird.
Hinter dem Teilchen wird eine Leere entstehen.
Infolge der großen Dichte-Differenz, werden die Gluonen von Außen mit Lichtgeschwindigkeit diesen leeren Raum attackieren, der immer wieder entstehen wird. Das alles wird zur Erhöhung des Druckes hinten dem Teilchen führen (Abb. 8).
Da unser Teilchen mit einer Beschleunigung fliegt, steigt der Druck vor dem Teilchen synchron mit der Geschwindigkeitserhöhung. Der Druck hinter dem fliegenden Teilchen wird ebenfalls zunehmen, jedoch mit einer leichten Verzögerung. Die Verzögerungszeit hängt ab von der Geschwindigkeit der Bildung des Leerraumes hinter dem Teilchen und von der Reaktionszeit des Vakuums an eine Änderung des Druckes.
Die Reaktionszeit hat einen konstanten Wert, der nur von den Eigenschaften des Vakuums abhängig ist.
Aufgrund der Tatsache, dass sich das Teilchen mit einer Beschleunigung bewegt, wird der Anstieg des Druckes P2 vor dem Partikel den Druckanstieg hinter dem Teilchen P1 ständig übersteigen, was letzlich zu einer Verringerung der Beschleunigung des fliegenden Teilchens führt.
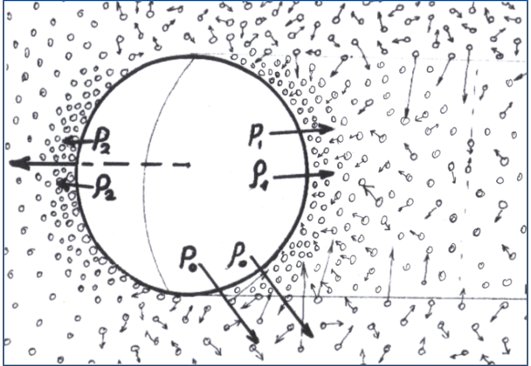
Abbildung 9: Ohne Beschleunigung werden die Drücke von beiden Seiten gleich sein
Sobald die Beschleunigung annuliert wurde, werden die Drücke von beiden Seiten gleich sein und das Teilchen wird, wenn keine anderen Kräfte auf es einwirken, unendlich lange mit der gleichen Geschwindigkeit weiterfliegen (Abb. 9).
Wenn wir jetzt eine äußere Kraft gegen die Flugrichtung des Teilchens ausüben, geschieht Folgendes:
Wie wir nun wissen wird ein Teilchen, das sich im Flug befindet, ständig, sowohl von vorderer als auch von hinterer Seite, von Gluonen mit erhöhter Dichte begleitet.
Bei plötzlicher Verzögerung des Teilchen-Fluges, fliegen die Gluonen ungestört weiter. Die Dichte und auch der Druck des Vakuums vor dem Teilchen werden proportional zur Geschwindigkeit der Flugabnahme sinken. Die Dichte und der Druck hinter dem Partikel werden entsprechend zunehmen.
Wegen dieser Druckdifferenz (P2 < P0) entsteht eine Kraft, die der Kraft der Hemmung widerstehen wird. Diese Kraft wird als Trägheitskraft bezeichnet.
Die Trägheitskraft bildet sich somit zu dem Zeitpunkt der Entstehung der Körperbewegung oder der Änderung seine Geschwindigkeit. Diese Kraft ist gegen die Änderung der Geschwindigkeit des Körpers ausgerichtet und hängt ab von Masse und Geschwindigkeit der Änderung des Körperzustandes. Das sind die Eigenschaften der Trägheit.
Dies ist ein sehr wichtiger Punkt, um zu verstehen, warum es keine Reibung zwischen einem sich bewegenden materiellen Körper und Gluonen gibt. Reibung entsteht nur, wenn ein Körper, der Trägheit besitzt, mit einer anderen Substanz, die ebenfalls Trägheit besitzt, in Wechselwirkung tritt.
Daher wird jedes Objekt, sei es ein Atom, ein materieller Körper oder ein Planet, das sich durch das Vakuum bewegt, dadurch nicht verlangsamt. Und dies ist eine sehr wichtige Eigenschaft des Vakuums, die es unserem Universum ermöglicht, unendlich lange zu existieren!
Um weitere Missverständnisse hinsichtlich der Umverteilung der Partikelgeschwindigkeiten nach deren Kollisionen zu vermeiden, möchte ich Sie auf zwei Arten von Partikeln aufmerksam machen:
- Gluonen, die keine kinetische Energie haben.
- Alle anderen Teilchen mit den Trägheitskräften.
Wie wir wissen, tragen alle Teilchen außer Gluonen im Flug zwei Bewegungskomponenten:
- Der Impuls, oder die Energiemenge eines Materialpunkts, der gleich dem Produkt der Masse des Materialpunkts durch seinen Geschwindigkeitsvektor ist.
- Die Trägheit die eine Eigenschaft jedes Körpers ist, seine geradlinige, gleicmäßige Bewegung aufrechtzuerhalten, bis eine andere Kraft auf ihn einwirkt.
Diese beiden reflektierenden Geschwindigkeitskomponenten sind nachstehend gezeigt, die bei der Kollision zweier Teilchen mit Trägheit und gleichen Massen gebildet werden (Abb. 10).
UP: Impulsvektorkomponente der Geschwindigkeit.
UTr: Trägheitsvektorkomponente der Geschwindigkeit.
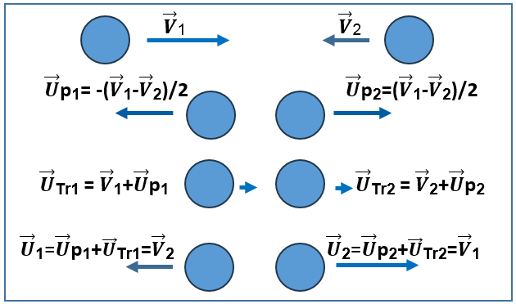
Abbildung 10: Umverteilung der Impuls- und Trägheitskomponenten nach einer zentralen Kollision zweier aufeinander zu fliegender Teilchen mit kinetischer Energie
Die Umverteilung der Impulse zum Zeitpunkt der Kollision erfolgt sofort, während die Umverteilung der Trägheit in einer bestimmten Zeit erfolgt, die als Reaktionszeit des Vakuums bezeichnet wird und die später erläutert wird.
Die Formeln geben die Vektorsumme der Geschwindigkeiten an, deren Vorzeichen von der Richtung ihrer Bewegung abhängt.
Nun sind wir bereits ausreichend vorbereitet, um zu verstehen, wie Atome entstehen und welch Mechanismen bei ihrer Entstehung beteiligt sind.
Wie wir bereits wissen, beginnt das Quarkteilchen aufgrund der vorhandenen Ausstülpungen im Vakuum zu rotieren und erreicht die uns bekannte Geschwindigkeit von 2,85 · 10^10 min^-1. Als Folge dieser gleichen Ausbuchtungen wird das angrenzende Vakuum in diese Quarkrotation hineingezogen.
Die Fliehkraft (Zentrifugalkraft) wirkt auf die Gluonen nicht aus, weil sie, wie wir schon wissen, keinen Gesetzen der Trägheit unterliegen.
Deswegen fliegen die Gluonen, die mit ihren hohen Lineargeschwindigkeiten um den Quark bewegen, nicht auseinander, sondern bleiben auf ihren Schichten der Drehung. Ihre Abstände zum drehenden Teilchen hängen nur von der Druckdifferenz des Vakuums ab.
Je dichter sich die Gluonen zum rotierenden Quark befinden, desto mehr richten sie sich der Rotationsgeschwindigkeit des Quarks ein. Ihre linearen Geschwindigkeiten nähern sich der Drehzahl des Quarks.
Als Folge, fällt den näher am Quark liegenden Druck 𝑷𝟏 des Vakuums gegenüber dem äußeren Druck 𝑷𝟎. Die äußeren Gluonen des Vakuums (infolge der Druckdifferenz), die senkrecht zum rotierenden Teilchen fliegen, bekommen von den rotierenden und anders (waagerecht) ausgerichteten Gluonen fast keinen Widerstand.
Mit der Zeit werden immer mehr Gluonen sich um das Quark konzentrieren, was zur Vergrößerung der Gluonen Dichte führt.
Eine Zunahme der Dichte führt dazu, dass die Anzahl der Gluonen, die den Angriffen äußerer Gluonen standhalten müssen, nach und nach zunimmt. Es wiederum führt zur Steigerung des Innendruckes 𝑷𝟏. Eine solche Zunahme der Dichte von rotierenden Gluonen und gleichzeitig eine Zunahme des Druckes werden fortgesetzt, bis den Druck 𝑷𝟏 gleich dem äußeren Druck 𝑷𝟎 wird.
Infolge der Wechselwirkungen zwischen den Teilchen, entsteht um das Quark einen verdichteten kreisförmigen Fluss aus den Gluonen (Abb.14).
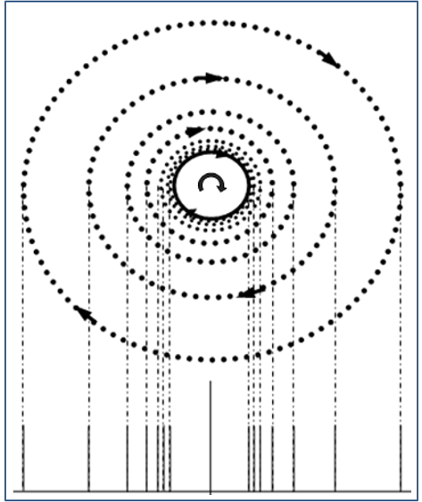
Abbildung 14: Um das Quark entsteht eine verdichtete Hülle aus Gluonen
Da die Winkelgeschwindigkeit des Quarks ungeheuer groß ist (𝟒, 𝟕𝟔 ⋅ 𝟏𝟎^𝟖 𝐬−𝟏), ist der Druckabfall am Anfang an sehr groß und daher nimmt die Vakuumdichte um das rotierende Gluon stark zu. Eine Erhöhung der Dichte des Vakuums setzt sich fort, bis sich der Innendruck des Vakuums mit dem Außendruck ausgleicht (𝑷𝟏 = 𝑷𝟎).
Weiter nach außen werden die rotierenden Geschwindigkeiten der Gluonen und damit auch die Dichte des Vakuums langsam fallen (Abb.14).
Je größer die Dichte des komprimierten rotierenden Vakuums um das Atom und je größer sein Volumen ist, desto größer ist die Bindungsenergie in ihm.
Die Formel zur Berechnung der Bindungsenergie lautet wie folgt:
E = pVc^2
Hier Sind:
c - Durchschnittliche Geschwindigkeit der Gluonen (Lichtgeschwindigkeit).
p - Die Dichte des komprimierten rotierenden Vakuums.
V - Das Volumen des komprimierten rotierenden Vakuums.
Da das Produkt aus Dichte und Volumen nichts anderes ist, als die Masse (m = pV) kommen wir zu der bekannten Formel von „Albert Einstein“:
E = mc^2
Durch die gegenseitige Beeinflussung solcher rotierenden Strömungen entstehen die Voraussetzungen für die Bildung verschiedenster Atome und Moleküle.
©Urheberrecht. Alle Rechte vorbehalten.
Wir benötigen Ihre Zustimmung zum Laden der Übersetzungen
Wir nutzen einen Drittanbieter-Service, um den Inhalt der Website zu übersetzen, der möglicherweise Daten über Ihre Aktivitäten sammelt. Bitte überprüfen Sie die Details in der Datenschutzerklärung und akzeptieren Sie den Dienst, um die Übersetzungen zu sehen.